Nietypowe przypadki

     Klasyczna formuła Wilks'a podaje współczynniki zależne od wagi ciała z dokładnością do 100 g.  Obejmuje zakres  40-205,9  kg dla mężczyzn i 40-150,9 kg dla kobiet. Zatem waga ciała moze trojako odbiegać od istniejącej tabeli współczynników:

• waga ciała jest mniejsza niż uwzględniona w tabeli

• waga ciała jest wieksza niż w tabeli

• waga ciała podana jest z większa dokładnością niż 100 g.

Dokładność większa od nominalnej może również występować w przypadku wagi zbyt małej i zbyt dużej. W tym ostatnim przypadku, ze względu na sposób stosowania formuły Wilks'a, nie bierzemy jej pod uwagę.

Różnice między interpolacją liniową a rzeczywistymi współczynnikami

     Gdy waga ciała jest dokładniejsza niż 100 g, należy użyć interpolacji liniowej do wyliczenia właściwego współczynnika Wilksa. Interpolacja liniowa jest tylko przybliżeniem mającym zapewnić lepsze porównanie poziomu sportowego zawodników niż brak zróżnicowania współćzynników pomimo różnej wagi ciała. W rzeczywistości zawodnik ze współczynnikiem interpolowanym otrzymuje zawyżoną ilość punktów.
  

 Rys. 1. Przebieg współczynników dla kobiet i mężczyzn

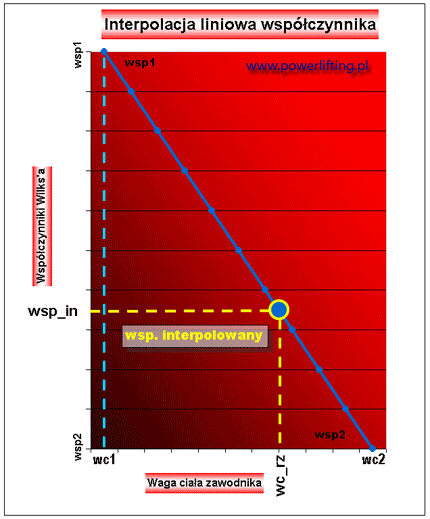
     Z rys.1. widać, że wraz ze wzrostem wagi ciała różnica pomiędzy współczynnikami w określonym przedziale maleje. Powoduje to, że wartość rzeczywistych współczynników maleje szybciej niż liniowe przybliżenie - co widać wyraźnie na rys.2.: wartość wsp_in jest większa od wartości wsp_rz. Praktycznie przyjmujemy, że różnica wsp_in - wsp_rz, jest pomijalnie mała i nie uwzględniamy jej w wyliczeniach.
W jednym przypadku można wziąć ją pod uwagę: gdy dwóch zawodników uzyskuje ilość punktów, z których jeden z nich miał wyliczoną wartość poprzez interpolację liniową, to lepszy jest zawodnik ze współczynnikiem wziętym sztywno z tabeli. Na zawodach różnica wsp_in - wsp_rz nie jest brana pod uwagę i obaj zawodnicy będa równo traktowani pod wzgldem zajętego miejsca w punktacji na najlepszego zawodnika.

Należy przy tym pamiętać, że obecne współczynniki, podane z dokładnością do 4-go miejsca po przecinku, są przybliżeniem faktycznie wyliczonych. Dlatego interpolacja najlepiej sprawdza się dla zawodników z niskich kategorii, w których wzrost wagi ciała o 100 g powoduje stosunkowo duży spadek współczynnika - patrz rys.1.

Rys. 2. Porównanie współczynnika rzeczywistego i inetrpolowanego

Uśrednianie współczynników

         Najczęściej występującym przybliżeniem współczynników jest ch uśrednienie. Może wystąpić w przypadku stosowania na ważeniu wagi dziesiętnej z wyraźną podziałką co 100 g lub przy zastosowaniu wagi elektronicznej podającej wskazania z dokładnością do 50 g. W pierwszym przypadku ustawienie obciążnika na niższej wadze powoduje podwyższenie "dziubka", zaś ustawienie na wyższej o 100 g obniża ruchomy "dziubek" poniżej "dziubka" stałego. Zawodnik może wtedy domagać się wpisania wagi uśredniowej czyli podzielnej przez 50 g. W przypadku wagi ciała podzielnej przez 50 g i niepodzielnej przez 100 g, stosujemy zwykłą średnią arytmetyczną najbliższych współczynnków z tabeli dla wagi lżejszej i cięższej od rzeczywistej:

wsp_rzecz =  0,5 * (wsp_większy + wsp_mniejszy)

Na rys. 3. widac przykład takiego uśrednienia dla wagi ciała równej 70,25 kg. Z tabeli znajdujemy współczynnik dla wagi 70,2 kg - wsp_większy = 0,7478, oraz wsp_mniejszy = 0,7469. Podstawiając do wzoru otrzymujemy:
wsp_rzecz = 0,5 * (0,7478 + 0,7469) = 0,5 * 1,4947 = 0,74735.  Taki współczynnik przyjmujemy do obliczenia punktów Wilks'a. 

Rys. 3. Schemat uzyskiwania współczyników dla dokładności 50 g

Interpolacja liniowa praktycznie

        Dla wag elektronicznych mogących podawać wynik z dokładnością do 10 g stosujemy standardową interpolację liniową. Praktycznie, jak widać z rys.4. dzielimy różnicę pomiędzy najbliższymi współczynnikami z tabeli (jak opisano wyżej) przez 10. Uzyskany wynik mnożymy końcówkę wagi w postaci cyfry  i odejmujemy od wyższego współćzynnika.
Dla przykładu obliczymy współczynnik dla wagi 70,23. Najbliższy większy współczynnik z tabeli wynosi 0,7478, najbliższy mniejszy - 0,7469. Różnica między nimi wynosi 0,0009. Podzielona przez 10 wyniesie: 0,0009 / 10 = 0,00009.  Ten wynik mnożymy przez ostatnią cyfrę rzeczywistej wagi ciała - 3: 0,00009 * 3 = 0,00027. To jest wartość pomniejszenia współczynnika dla wagi 70,2 kg. Teraz wystarczy tę wartość odjąć od wartości większego współczynnika, by otrzymać współczynnik interpolowany: 0,7478 - 0,00027 = 0,74753. Co widać na rys.4.

Rys. 4. Schemat uzyskiwania współczyników dla dokładności 10 g

Interpolacja liniowa teoretycznie

     W poprzednim przykładzie zastosowaliśmy klasyczną interpolację. Z rys.5. dobrze widać graficzne zależności pomiędzy wagą rzeczywistą i współczynnikiem interpolowanym a najbliższymi współczynnikami wziętymi z tabeli. Na podstawie twierdzenia Talesa szybko otrzymujemy proporcję:

odcinek wc2-wc_rz pozostaje w takiej proporcji do odcinka wc2-wc1 jak odcinek wsp2-wsp_in do odcinka wsp2-wsp1.

Rys. 5. Schemat obliczenia współczynnika interpolowanego

Określając długości odcinków jako różnicę wartości znanych współczynników i wagi ciała otrzymamy:

 długość odcinka wc2-wc_rz wynosi wc_większa - wc_rzecz
 długość odcinka wc2-wc1 wynosi wc_większa - wc_mniejsza
 długość odcinka wsp2-wsp_in wynosi wsp_{interpolowany} - wsp_mniejszy
 długość odcinka wsp2-wsp1 wynosi wsp_większy - wsp_mniejszy

dla uproszczenia dalszych obliczeń pozostawię w indeksach tylko jego pierwsza literę

Zatem

 (wc_w - wc_r) * (wsp_w - wsp_m) = (wc_w - wc_m) * (wsp_i - wsp_m)

Co daje

a następnie

i ostatecznie otrzymujemy końcowy wzór na interpolację liniową

Można sprawdzić powyższy wzór na przykładzie wyżej:

wsp_i = 0,7469 + 0,7 * 0,0009 = 0,7469 + 0,00063 = 0,074735

Otrzymaliśmy więc dokładnie taki sam wynik jak w poprzednim przykładzie wychodząc z trochę innej proporcji.